Average vs. Linear Growth
Understanding probability can lead to clearer thinking during market volatility
Guest post by The Arbitrageur
The world of financial planning and personal finance is full of performance quotes for various financial assets quoted in yearly averages. While this provides a simple way to take a complicated topic and refer to the bottom line result quickly it unfortunately also lays the foundation for disappointment and unrealistic expectations for the future if the concept of average is not further explained because we all live our lives and make decisions day by day, not decade by decade. In this piece we will explore the following:
Probability
How linear growth and average growth are different
Why does this matter?
Volatility
Probability
Let's pretend you have a quarter that has 2 sides, heads, and tails. This quarter has an equal chance of landing as a heads or tails on any given flip. This would otherwise be known as a 50% probability. That all being said if you were to take that quarter out of your pocket and flip it twice you could get the following results on the flips:
2 Tails
1 Heads, 1 Tails
2 Heads
On a sample of only 2 flips, it is tough to say which outcome is more likely. If you were to do 100 flips or 1,000 flips the chances that you will end up with roughly the same amount of heads and tails are strong. Another way we could explain this is that the "average" 2 coin flips will yield 1 heads, and 1 tails result. The more times we flip a coin to demonstrate this the more true this statement will be. All this is to say that averages and therefore probabilities, in general, can be strong over a large set of data, but there can be significant variance over small sample sizes that will produce other outcomes within a given data set along the way.
Linear Growth and Average Growth are different
Linear growth is a simple calculation that over a given amount of time there will be a fixed rate of return that comes in on a predictable basis. For example, if we invest $100,000 and get a 4% fixed rate of return your sequence of returns will look like this:
In a linear growth scenario, there is no change in what you might make from year to year, and there is never a period where you check the balance of your accounts and see that you have lost money. You simply need to wait the allotted amount of time you selected upfront and you will get your rate of return on the back end.
By contrast "Average Growth" is calculated by finding the average growth experienced per year over a given period of time. An average is simply the sum of a series of numbers divided by the total number of inputs. For example:
Version 1: (8+8+8+8) / 4 = 32/4 = 8
The example above is simple, but there are many combinations of other numbers that can add up to be 32 over 4 numbers that can also be represented by the same average of 8. For example:
Version 2: (10 + (-5) + 7 + 20)/4 = (32) / 4 = 8
Version 3: ((-3) + 20 + (-5) + 20)/4 = (32) / 4 = 8
And so on….
If we take this concept away from basic math and apply it to the realm of financial planning using an annual growth rate of 8% per year with the numbers from the example above our compounding would look like this:
As you can see from above the numbers at the end of Y4 are all close to the same value with a small difference due to the phenomenon of compounding interest, but for the purpose of this explanation, we can consider close as adequate over a long time horizon.
Why does this matter?
Many investors are conditioned to think about the compounding interest required for their retirement projections in terms of linear growth, and this is only compounded by many financial projections using a linear growth rate to illustrate the value of their portfolios climbing steadily year by year. While this makes sense intellectually it also presents opportunities for misunderstandings between clients and the products that they use to generate growth for their retirement. These misunderstandings can lead to adverse outcomes such as general anxiety, selling at the wrong time for the wrong reason, and taking too much risk for their personal situation.
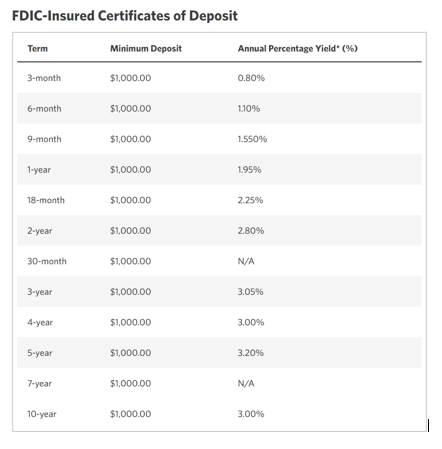
At this point, it would be fair to ask why anyone would sign up for "average growth" as illustrated above given the volatility of returns when they could just get linear growth instead? The simple answer here is that the growth rate offered by fixed instruments that can provide the "linear" growth explained above is far lower than the growth offered by the more volatile "average" growth instruments such as the stock market. For example here is a snapshot of current CD rates as of 5/10/2022:
If we were to purchase a 10 year CD at 3% per year your sequence of returns would look like this:
After 10 years of investing, you have $34,391 of profit on a starting investment of $100,000
Now let's review the historic returns of the market:
As you can see here the market has a historical return of 10.5% per year between 1926 and 2021 and most of the years in that sample have produced returns of 16% or more during that period of time. Interestingly there have only been 6/95 years that have produced within the "average" 8-12% return per year. If we were going strictly by the historical data on the preceding chart for forward expectations on earnings, we would say the following:
Chances you will return:
Said another way your chances of making money in any one year is 82.42%, with many of those positive return years yielding double-digit returns in a single year. If we now show our sequence of returns using the same method as before and an annual return of 10.5% you would return the following:
Using a simple 10.5% per year growth rate our excess return is as follows:
$271,408.08 – $134,391.64 = $137,016.36
You made $137,016.36 more over 10 years by earning an additional 7.5% per year. If we were to demonstrate this over a longer period of time, or with more money the results would be even more extreme.
Volatility:
While these returns are incredible wealth creators it is noteworthy to point out that the stock market does not produce returns on a linear basis, and many years see meaningful drawdowns along the way to compelling long-term gains. Take the following chart for example:
Over the measurement period of 1980 to 2021, the index returned an average of 9.4% per year and finished positive 76% of the time BUT the average intra-year drop was 14% during the measurement period. Taking 2020 as an example from recent memory that meant that although the index finished up 16% on the year, it was down 34% at the end of March 2020. For someone expecting "linear growth" as explained earlier this can be jarring, but that doesn't that the stock market is broken, or even that they will stay down or lose all their money if they keep holding. History would argue the exact opposite is true. Additionally, that same investor may be in the position where their financial goals require that they tolerate these swings in order to drive the returns that they desire long term to achieve what really matters for them.
Bringing it all together it is important to acknowledge that achieving success as an investor is a complicated proposition of managing emotions, selecting appropriate investments from a wide universe of options, and having realistic expectations along the way. It is important that investors know themselves, do a good job forecasting their future spending needs, and accurately communicate those needs to the people helping them to select the products they will be using. Lastly, it is important to recognize that while a linear experience is easier to handle emotionally, it is generally not lucrative enough to be a big part of the strategy for retirement-minded clients focused on long term growth unless they are exceptionally well funded and not dependent upon returns greater than 3% per year.